Covariance matrix
In probability theory and statistics, a covariance matrix (also known as dispersion matrix) is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector (that is, of a vector of random variables). Each element of the vector is a scalar random variable, either with a finite number of observed empirical values or with a finite or infinite number of potential values specified by a theoretical joint probability distribution of all the random variables.
Intuitively, the covariance matrix generalizes the notion of variance to multiple dimensions. As an example, the variation in a collection of random points in two-dimensional space cannot be characterized fully by a single number, nor would the variances in the x and y directions contain all of the necessary information; a 2×2 matrix would be necessary to fully characterize the two-dimensional variation.
Analogous to the fact that it is necessary to build a Hessian matrix to fully describe the concavity of a multivariate function, a covariance matrix is necessary to fully describe the variation in a distribution.
Contents |
Definition
Throughout this article, boldfaced unsubscripted X and Y are used to refer to random vectors, and unboldfaced subscripted Xi and Yi are used to refer to random scalars. If the entries in the column vector
are random variables, each with finite variance, then the covariance matrix Σ is the matrix whose (i, j) entry is the covariance
where
is the expected value of the ith entry in the vector X. In other words, we have
The inverse of this matrix, 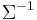 , is the inverse covariance matrix, also known as the concentration matrix or precision matrix.[1] The elements of the precision matrix have an interpretation in terms of partial correlations and partial variances.
, is the inverse covariance matrix, also known as the concentration matrix or precision matrix.[1] The elements of the precision matrix have an interpretation in terms of partial correlations and partial variances.
Generalization of the variance
The definition above is equivalent to the matrix equality
This form can be seen as a generalization of the scalar-valued variance to higher dimensions. Recall that for a scalar-valued random variable X
Conflicting nomenclatures and notations
Nomenclatures differ. Some statisticians, following the probabilist William Feller, call this matrix the variance of the random vector  , because it is the natural generalization to higher dimensions of the 1-dimensional variance. Others call it the covariance matrix, because it is the matrix of covariances between the scalar components of the vector
, because it is the natural generalization to higher dimensions of the 1-dimensional variance. Others call it the covariance matrix, because it is the matrix of covariances between the scalar components of the vector  . Thus
. Thus
However, the notation for the cross-covariance between two vectors is standard:
The var notation is found in William Feller's two-volume book An Introduction to Probability Theory and Its Applications, but both forms are quite standard and there is no ambiguity between them.
The matrix  is also often called the variance-covariance matrix since the diagonal terms are in fact variances.
is also often called the variance-covariance matrix since the diagonal terms are in fact variances.
Properties
For ![\Sigma=\mathrm{E} \left[ \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right) \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right)^\top \right]](/2012-wikipedia_en_all_nopic_01_2012/I/1811f942680a72974597be42c28d31d2.png) and
and 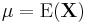 , where X is a random p-dimensional variable and Y a random q-dimensional variable, the following basic properties apply:
, where X is a random p-dimensional variable and Y a random q-dimensional variable, the following basic properties apply:
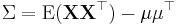
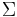 is positive-semidefinite and symmetric.
is positive-semidefinite and symmetric.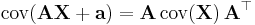
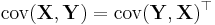
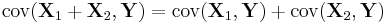
- If p = q, then
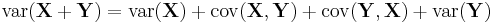
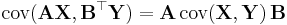
- If
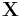 and
and 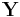 are independent, then
are independent, then 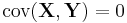
where 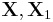 and
and 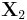 are random p×1 vectors,
are random p×1 vectors, 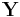 is a random q×1 vector,
is a random q×1 vector, 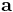 is q×1 vector,
is q×1 vector, 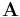 and
and 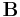 are q×p matrices.
are q×p matrices.
This covariance matrix is a useful tool in many different areas. From it a transformation matrix can be derived that allows one to completely decorrelate the data or, from a different point of view, to find an optimal basis for representing the data in a compact way (see Rayleigh quotient for a formal proof and additional properties of covariance matrices). This is called principal components analysis (PCA) and Karhunen-Loève transform (KL-transform).
As a linear operator
Applied to one vector, the covariance matrix maps a linear combination, c, of the random variables, X, onto a vector of covariances with those variables: 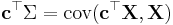 . Treated as a 2-form, it yields the covariance between the two linear combinations:
. Treated as a 2-form, it yields the covariance between the two linear combinations: 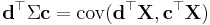 . The variance of a linear combination is then
. The variance of a linear combination is then 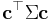 , its covariance with itself.
, its covariance with itself.
Similarly, the (pseudo-)inverse covariance matrix provides an inner product, 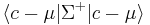 which induces the Mahalanobis distance, a measure of the "unlikelihood" of c.
which induces the Mahalanobis distance, a measure of the "unlikelihood" of c.
Which matrices are covariance matrices?
From the identity just above (let  be a
be a  real-valued vector)
real-valued vector)
the fact that the variance of any real-valued random variable is nonnegative, and the symmetry of the covariance matrix's definition it follows that only a positive-semidefinite matrix can be a covariance matrix. The answer to the converse question, whether every symmetric positive semi-definite matrix is a covariance matrix, is "yes." To see this, suppose M is a p×p positive-semidefinite matrix. From the finite-dimensional case of the spectral theorem, it follows that M has a nonnegative symmetric square root, which let us call M1/2. Let 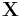 be any p×1 column vector-valued random variable whose covariance matrix is the p×p identity matrix. Then
be any p×1 column vector-valued random variable whose covariance matrix is the p×p identity matrix. Then
How to find a valid covariance matrix
In some applications (e.g. building data models from only partially observed data) one wants to find the “nearest” covariance matrix to a given symmetric matrix (e.g. of observed covariances). In 2002, Higham[2] formalized the notion of nearness using a weighted Frobenius norm and provided a method for computing the nearest covariance matrix.
Complex random vectors
The variance of a complex scalar-valued random variable with expected value μ is conventionally defined using complex conjugation:
where the complex conjugate of a complex number 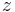 is denoted
is denoted 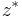 ; thus the variance of a complex number is a real number.
; thus the variance of a complex number is a real number.
If 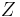 is a column-vector of complex-valued random variables, then we take the conjugate transpose by both transposing and conjugating, getting a square matrix:
is a column-vector of complex-valued random variables, then we take the conjugate transpose by both transposing and conjugating, getting a square matrix:
where 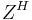 denotes the conjugate transpose, which is applicable to the scalar case since the transpose of a scalar is still a scalar. The matrix so obtained will be Hermitian positive-semidefinite,[3] with real numbers in the main diagonal and complex numbers off-diagonal.
denotes the conjugate transpose, which is applicable to the scalar case since the transpose of a scalar is still a scalar. The matrix so obtained will be Hermitian positive-semidefinite,[3] with real numbers in the main diagonal and complex numbers off-diagonal.
Estimation
The derivation of the maximum-likelihood estimator of the covariance matrix of a multivariate normal distribution is perhaps surprisingly subtle. See estimation of covariance matrices.
Probability density function
If a vector of n possibly correlated random variables is jointly normally distributed, or more generally elliptically distributed, then its probability density function can be expressed in terms of the covariance matrix.
See also
- Estimation of covariance matrices
- Multivariate statistics
- Sample covariance matrix
- Gramian matrix
- Eigenvalue decomposition
- Quadratic form (statistics)
- Sum of normally distributed random variables
References
- ^ Wasserman, Larry (2004). All of Statistics: A Concise Course in Statistical Inference. ISBN 0387402721.
- ^ Higham, Nicholas J.. "Computing the nearest correlation matrix—a problem from finance". IMA Journal of Numerical Analysis 22 (3): 329–343. doi:10.1093/imanum/22.3.329.
- ^ Brookes, Mike. "Stochastic Matrices". The Matrix Reference Manual. http://www.ee.ic.ac.uk/hp/staff/dmb/matrix/expect.html.
Further reading
- Weisstein, Eric W., "Covariance Matrix" from MathWorld.
- van Kampen, N. G. (1981). Stochastic processes in physics and chemistry. New York: North-Holland. ISBN 0444862005.
- "Covariance matrix". AI Access Glossary of data modeling. http://www.aiaccess.net/English/Glossaries/GlosMod/e_gm_covariance_matrix.htm#Animation_covariance%20matrix.
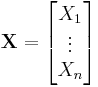
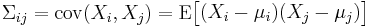
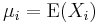
![\Sigma
= \begin{bmatrix}
\mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\
\mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
\mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]
\end{bmatrix}.](/2012-wikipedia_en_all_nopic_01_2012/I/58572fa5b05e778f5a5eff9ec1b3ddb6.png)
![\sigma^2 = \mathrm{var}(X)
= \mathrm{E}[(X-\mathrm{E}(X))^2] = \mathrm{E}[(X-\mathrm{E}(X))\cdot(X-\mathrm{E}(X))].\,](/2012-wikipedia_en_all_nopic_01_2012/I/6b790c0ee7f3b205075c68ce048aa9a4.png)
![\operatorname{var}(\textbf{X})
=
\operatorname{cov}(\textbf{X})
=
\mathrm{E}
\left[
(\textbf{X} - \mathrm{E} [\textbf{X}])
(\textbf{X} - \mathrm{E} [\textbf{X}])^\top
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/f8cb85080acf88e54c194ad48bab8527.png)
![\operatorname{cov}(\textbf{X},\textbf{Y})
=
\mathrm{E}
\left[
(\textbf{X} - \mathrm{E}[\textbf{X}])
(\textbf{Y} - \mathrm{E}[\textbf{Y}])^\top
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/5393cfe54a257747ea8335e92d4ce5ee.png)
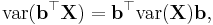
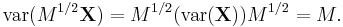
![\operatorname{var}(z)
=
\operatorname{E}
\left[
(z-\mu)(z-\mu)^{*}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/4db5552832ee20b19f0ef057887f2162.png)
![\operatorname{E}
\left[
(Z-\mu)(Z-\mu)^{H}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/6911ea19c5eb10d60575dabe69b4fc64.png)